Motivation
While de-identification by removing explicit identifiers is the first step that we take towards the privacy protection, we consider the cases when the approach may fail to provide the sufficient level of protection specifically when records associated to the individuals contain characteristics or combinations of characteristics that are rare if not unique and make them identifiable even in the large crowds and even in the cases when data query responses are restricted to aggregate statistical results only.
CanDIG provides an additional layer of privacy that enable to perform different data analyses in a privacy-preserving way. CanDig does that by the implementing the notion of differential privacy. That is, to learn as much as possible about a group while learning the minimum possible at the individual-level.
With differential privacy, a data user can perform analyses collectively over the available data in a way that lets him glean useful notions about the associated group of individuals as a whole. But anything about a single, specific one of those participants can’t be learned.
CanDIG implements the extension of differential privacy in two ways. First, it facilitates the choice of ε in a more meaningful way thereby simplifying the application of differential privacy in practice. Second, it supports privacy-preserving data analyses in distributed settings. This is an important requirement in modern biomedicine research since data collected at one site are usually sparse and insufficient to draw significantly reliable scientific conclusions. CanDIG ensures that the required level of privacy be achieved when analysis be performed collectily over the data partitions residing distributively.
Why Differential Privacy
Because it is future proof. Backed by a formal proof, Differential Privacy gives a specified level of assurance that no participant of a data analysis will be affected in privacy perspective irrespective of what other datasets, studies, or information sources are or will become available in future. This also implies that sensitive data can readily be made available for useful analysis without such practices as data usage agreement or data protection plans.
Given a randomized computation M, Differential Privacy requires that the change in the probabilities that any given output is produced using a given input and by its neighbouring datasets (construced by adding to or removing a record from the input dataset) is at most a multiplicative factor e. In other words, the ratio of the probabilities that M produces a given output when an individual opts in or out of a study is upper bounded by e. The probabilities are taken over random choices made by M.
The parameter e gives a way to precisely control and quantify the privacy loss guarantees. Lower the e causes stronger privacy guarantees as it limits the effect of a record on the outcome of the computation and hence may produce the output with lower accuracy level. This leads to to the fact that the choice of e is cruicial but not trival since $\epsilon$ is taken in the context of a relative quantification of privacy and does not easily relate to an absolute privacy measure in practice.
CanDIG supports differentially private data analysis by implementing differentially privacy in simple low-level computational constructs over the data. The low-level queries are made differentially-private using laplace mechanism. A laplace mechanism computes the original results from given input and adds random noise from 0-centered laplace distribution. The scale of the distribution is determined by the sensitivity of the computation (i.e. the maximum amount by which the original output changes when a computation is performed over a dataset and a neighbouring dataset) and by the choice of privacy settings e.
This allows privacy loss over the composition of multiple differentially private mechanims be quantified and hence complex data mining can be made with privacy-preserving way.
Privacy-Preserving Decision Tree Induction over 1000 Genome Data
For experimentation purposes, we implemented differentially-private decision tree induction algorithms originally presented by Jagannathan et. al [ref] under CanDIG. A Decision tree Induction builds classification or regression models in the form of a tree structure. Given a set of pre-classified instances as input, the algorithm decides which of the so far unused attributes is best to split on, uses the attribute values to split the instances into smaller subsets, and recurses over the resulting subsets until the instances in all subsets have homogenous class attribute values or a pre-specified condition is met. The final result is a tree with decision nodes and leaf nodes representing the attributes used to classify the attribute at the corresponding recursive step and the classification results respectively.
We report our findings over 1000 Genome data. More specifically, we considered the problem of classifying individuals into one of the given ancestral populations based on the single-neucleotide polymorphisms (SNPs). The SNPs overlapping xenobiotic metabolisim and human pigmentation gene regions e.g. TYR, OCA2, DCT etc. were considered. It was noticed that not all the SNPs are equally informative and further filteration was therefore performed based on their allele frequencies in each population.
ID3 (Iterative Dichotomiser 3)
ID3 is a classical decison tree induction method. It uses a heuristic that is based around the goal of constructing a tree with the purest possible leaf-nodes but the minimum possible depth. ID3 does that by greedily choosing an unused attribute at each split that leads to the data subsets with maximum purity. The purity is measured using the concept of information gain. That is, the change in the amount of information needed to classify the instances of a current dataset partition, to the amount of information required to classify them if the current dataset partition were to be further partitioned on a given attribute.
We obtained the differentially private ID3 algorithm by replacing original low-level queries over training instances with equivalent laplace mechanisms. e privacy loss guarantees in the overall tree induction is ensured by taking into account the composibility of these e-differentially private low-level query functions. Following the observation of Jagannathan et. al [ref], the e-differentially private queries posed to extend the different nodes at a particular level of the tree takes disjoint subsets of data. Therefore the combined outputs are not more diclosive about an individual than the individual query results and hence gives e-differential privacy.
Queries posed at different hierarchical levels use sequential compositition. That is, they operate on the same data and the query functions at particular hierarchical level are composed of the query functions at the previous level. Assume, if the depth of the tree is d and privacy loss at each level is e then the overall privacy loss is d e.
[Data Ingestion and Differentially private Federated Classification needs first implementation] (ga4gh)
Random Decision Trees
The random decision tree classifier presented in Jagannathan et. al is composed of an ensemble of random decision trees (RDT). As written in the paper, a random decision tree is built by repeatedly splitting the data by a randomly chosen feature. After a random tree structure is built, the training data is filtered through the tree to collect counts of each class label at the leaf nodes. To classify an individual, its data is passed through the tree until a leaf node is reached. The individual is classified as the class with the highest count at the leaf node. To privatize the classifier, laplacian noise is added to the counts.
An of ensemble of these random trees is used to increases the robustness of the classifier. The counts are added up from each individual tree and the highest sum is used to classify a data point.
In the case of the 1000 genomes data, the features of an individual were based on the SNPs at certain locations in the genome that were informative of their ancestral population [ref]. The data in the paper (~20) had relatively fewer features than our dataset (~180). This caused the RDT ensembles to produce poor classification results. To improve the results, PCA was run on the data to product features that were more informative.
Building an ensemble of trees of the top 40 principal components with a maximum height of 10 seemed to produce the best results with an accuracy of 74.48. Adding noise with a very low epsilon of 0.0001 reduced the accuracy to 22.32 while an epsilon of 0.15 only reduced the accuracy to 65.83.
mean std
accuracy accuracy
ncomponents 40 40
ntrees 10 10
max_h 10 10
eps
-1.0000 74.484127 3.632744
0.0001 22.321429 10.616327
0.0010 21.607143 12.978305
0.0100 42.480159 10.975078
0.0200 51.607143 6.281403
0.0500 63.432540 3.605242
0.1000 65.793651 2.806267
0.1500 65.833333 2.841442
0.3000 67.301587 3.019191
5.0000 77.202381 1.760838
10.0000 77.658730 1.530844
Accuracy vs epsilon
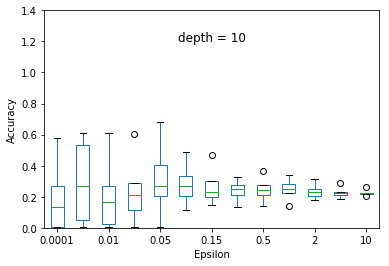
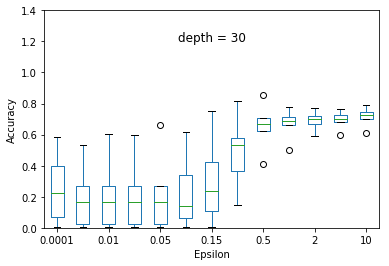
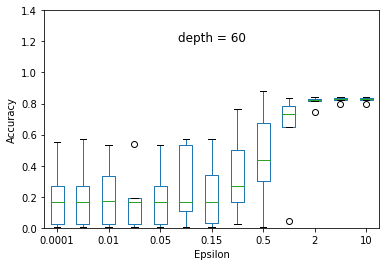
We experimented the effect of e and d over the accuracy of ID3 classification. At each particular setting of e and d, we repeated the experiment 40 times and diplayed the results using a five-number summary(i.e. minimum, first quartile, median, third quartile and maximum).
Overall, the results follow the s-shaped growth. That is, for certain range of e, the accuracy grows dramatically(e.g. 0.15 to 1.0 when depth is set to 30). Increasing or decreasing the e values beyond that range does not significantly effect the accuracy level.
 |
 |
 |
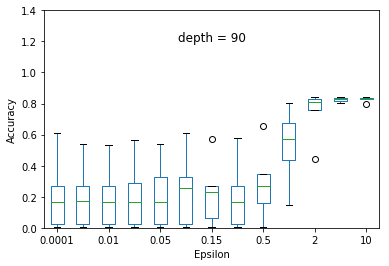 |
As expected, the accuracy level is also effected by d. For some fixed e, increasing d to significantly high values causes small privacy loss budget to be allocated to each query and hence high amount of noise to be added to each query results. This causes low accuracy achieved at most of the e settings but when d is set to relatively very low value (e.g. d = 5) constructs highly generalized model and hence an underfit to the data.
Adverarial model
While differential privacy backed by formal proof seems a perfect solution, the choice of e still makes the proper application of differential privacy in practice difficult. For example, adhering to a jurisdiction’s privacy law, the goal of a data curator is to achieve the privacy to the level that no data participant is individually identified. Interpreting the values of e to achieve this goal in different data summaries is not simple yet important. Note that setting e to singificantly low values may be required in a number of scenarios but not always a panacea since it also controls the accuracy with which a data analysis can be made and hence may leave the data over-protected but useless at the same time for any research purposes.
CanDIG supports the choice of e for proper privacy protection by interpretating it in a more meaningful way thereby assuming the presence of a very strong adversary [ref] who has access to a dataset D consisting of |D| records. Consider a study in which |D|-1 of the individuals participated. Let the prior beliefs of the adversary about the participance of an individual on the study is 1/|D|. That is, the absence of an individual in the study is equally probable. Given the noisy results of the study, the adversary may learn that some of the individuals are less likely to participate in the study than others. Our goal is to choose e in a way that the associated disclosure risk about the participation of an individual is upper bounded by a pre-specified threshold B.
